Ivan Perez Avellaneda
I hold a Ph.D. degree in electrical engineering from the University of Vermont, M.Sc in economics and a B.Sc. and License degree in mathematics from the Pontificia Universidad Católica del Perú.
During my doctoral studies I worked on inifinite dimension real analysis, nonlinear control theory, noncommutative algebra and optimization. Specifically, my research lies in the field of reachability analysis of nonlinear systems which involves extending optimization methods to Chen-Fliess series. Prior to this, I worked on algebraic geometry in mathematics and debt-control in economics.
Knowledge is a conjecture susceptible of improvement- K.Popper
Projects
Reachability of Systems
A reachable set is the set of states of a system
as a result of a set of inputs and initial conditions.
Knowing the possible reachable sets ahead of the execution
of the system is useful for the plannification and control of its outputs.
Popular offline methodologies to compute these sets for nonlinear systems
are the Hamilton-Jacobi
approach, Mixed-Monotonicity and set-progration.
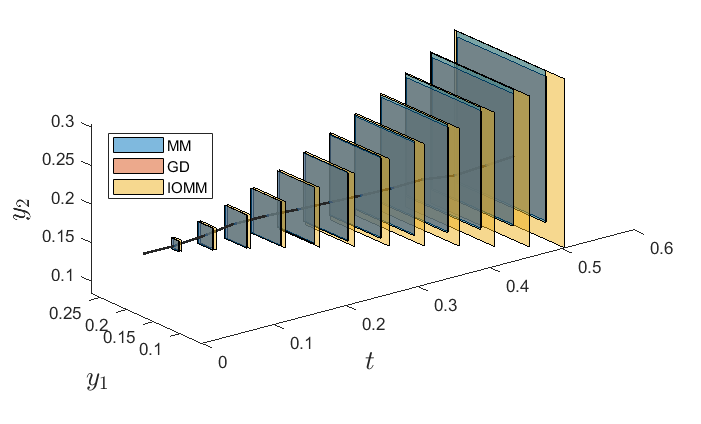
My contributions to this topic are the following: first, I provided a reachable set overestimation
using interval arithmetics. Second, I extended the Mixed-Monotonicity
approach to Chen-Fliess series to configure an Input-Output
Mixed-Monotonicity (IOMM) framework. Third, I extended differential analysis
tools to Chen-Flies series to improve the IOMM outcome.
Relevant publications:
Sponsors:
Optimization of Chen-Fliess Series
The applications of optimization is pervasive over all scientific disciplines.
In nonlinear optimization two techniques standout:
line search and trust regions.
These are related to first and second order derivatives, respectively.
The advantage of the first approach is that it
only uses the gradient while the second requires the computation
of the Hessian matrix. The second approach is more accurate when
the approximation to the second order of the Taylor polynomial
is better.
My contributions to this topic are the following:
first, I provided closed forms of real analysis tools such as the Fréchet,
Gâteaux derivative, the gradient and Hessian
of Chen-Fliess series.
Second, I proved the first and second order
Mean Value Theorem for Chen-Fliess series using the closed form of
the Chen-Fliess series of the sum of two inputs rather than the
classical approach by the chain rule.
This allows a Taylor expansion of Chen-Fliess series.
Third, I implemented the Gradient Descent and Newton-Raphson
algorithm to optimize Chen-Fliess series.
Relevant publications:
Sponsors:
Differential monoids
I introduced the theory of differential monoids to the literature
to formalize the concepts of differential analysis of Chen-Fliess series.
This helps provide a closed-form of the Fréchet and Gâteaux derivative
by building a bridge between noncommutative algebra and analysis and extends
differential calculus to Chen-Fliess series. For this, alphabet is extended
with the introduction of differential letters that represent the action
of differentiation. Then a differential monoid is constructed by defining a
derivation operator on the free monoid. This operator satisfies the Leibniz rule.
Several properties of the derivation operator are provided including
its interaction with the shuffle product that show the combinatorial nature
of the differential monoid. An important property deduced from this theory
is that when the Fréchet and Gâteaux derivatives exist, they are
equivalent, algebraically.
The main result is a commutative diagram established
between the Gâteaux or Fréchet derivative and the language derivative defined on the differential monoid.
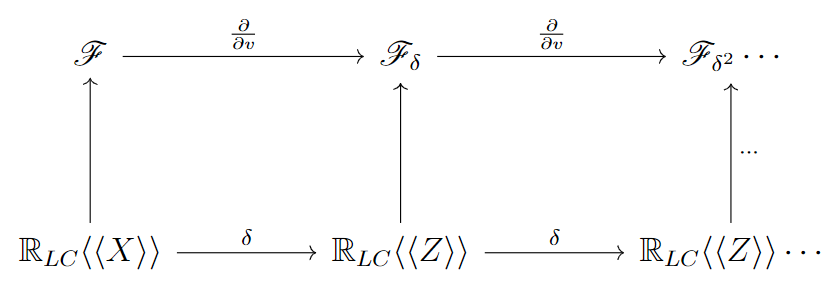
In Fig.3, the space of Chen-Fliess series is denoted by \(\mathscr{F}\) and the space of all locally convergent series is denoted by \(\mathbb{R}_{\text{LC}}\langle\langle X \rangle\rangle\), and \(Z\) is the alphabet \(X\) with the differential letters. This diagram shows that the Gâteaux derivative can be computed by means of the language derivation on the differential monoid. This is, the derivative of Chen-Fliess series is equal to the Chen-Fliess series of the derivative of its generating series.
Relevant publications:
Sponsors:
Publications
Conferences
Journals
Talks
Thesis and Dissertation
Software
ChenFliessSeries.jl
The ChenFliessSeries.jl is a library in the Julia programming language to simulate the output of a nonlinear control affine system by means of the Chen-Fliess series. It's the adaptation of the CFSpy package in Python to Julia. The package computes the list of coefficients of the Chen-Fliess series and the list of iterated integrals up to a truncation length.
First release: January, 2026
Currently version: 1.0.0.
License: MIT
CFSpy
The Chen-Fliess Series Python (CFSpy) package is a set of functions used to simulate the output of control systems by means of Chen-Fliess series. CFSpy computes the list of coefficients of the Chen-Fliess series and the list of iterated integrals up to a truncation length. The package, also, provides functions that compute single iterated integrals and Lie derivatives. CFSpy is implemented in Python in the object-oriented paradigm.
First release: July, 2024
Currently version: 1.2.3.
License: MIT
CFS-toolbox
The CFS-toolbox is a library of scripts written in MATLAB to simulate the output of a nonlinear control affine system by means of the Chen-Fliess series. It's the foundation of the CFSpy package in Python and ChenFliessSeries.jl in Julia. The package computes the list of coefficients of the Chen-Fliess series and the list of iterated integrals up to a truncation length.
First release: September, 2023
Currently version: 1.0
License: MIT